在聊聊编译原理（一）中，我们详细的介绍了编译器工作流程中的第一个步骤：词法分析。在这篇文章中，我们开始学习编译过程中的第二个重要步骤：语法分析。

语法分析

如果把词法分析看作为字母组合成单词的过程，那么语法分析就是一个把单词组合成句子的过程。正如在词法分析中使用正则表达式来描述词法的规则一样，我们在语法分析中使用一种比 RE 表达能力更强的工具——上下文无关文法，来描述语言的语法规则。我们可以把某一种语言看成无数个符合语法规则的句子的集合，根据给定的上下文无关文法我们可以判断某一个 Token 串是否符合某个语法规则；如果符合，那么我们可以把此文法和对应输入的 Token 串组合起来生成一个句子。整个流程如下图所示：

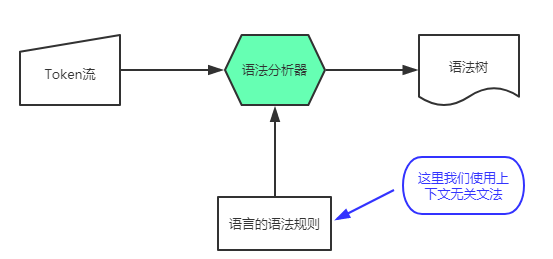
上下文无关文法

上下文无关文法（context-free grammar, CFG），是一种用来对某种语言进行形式化的、精确的描述的工具。有了这个工具，我们就可以很方便的定义一种语言的语法了。CFG 是一个四元组（N, T, P, S），下面我们看一下 CFG 的组成：

N 是非终结符的集合；
T 是终结符的集合；
P 是一条产生式规则；
S 是（唯一的）开始符号；

这样描述不免抽象，下面我们来看一个例子。（除了下面的这种描述语法，你可能还看过其它的描述 CFG 的语法，其中比较有名的是巴科斯范式，它们的本质其实是一样的，都是对 CFG 的四元组的描述。）

S –> AB
A –> aA | ε
B –> b | bB

其中 S A B 就是非终结符，代表可以继续扩展或产生的符号；a b ε是终结符，表示其无法再产生新的符号了，其中ε表示一个空句子；上面的每一行就是一个产生式规则，代表了一种非终结符的转移方式；而 S 就是开始符号。

只有终结符的符号串称为句子（sentence）。经过观察可知，这个语法所能推导出的所有句子的集合为：

A : { ε, a, aa, aaa, ... }
B : { b, bb, bbb, ... }
S : { b, bb, bbb, ..., ab, abb, ..., aab, aabb, ... }

分析方法简介

给定文法 G 和句子 s，回答 s 是否能够从 G 推导出来，这是在语法分析器内部所要实现的功能，这里我们开始讨论语法分析器内部要如何才能实现这一功能。

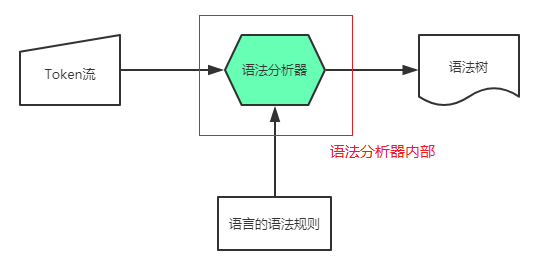
在这里我们讨论的是语法分析器内部为了对 G 和 s 进行判断所实现或者使用到的数据结构与算法，下面介绍几种常用的算法：

1. 自顶向下分析算法

自顶向下分析就是从起始符号开始，不断的挑选出合适的产生式，将中间句子中的非终结符的展开，最终展开到给定的句子。它的核心思想在于，当我们从左往右匹配这个句子的时候，每匹配一次需要从上往下遍历一次这个 CFG 从而找到合适的产生式，所以被称为自顶向下分析算法。我个人认为这种方法有点类似于“穷举法”（试错法），因为它的本质是不断的使用产生式规则来发现符合这个句子的语法。

不过自顶向下分析并不是无脑穷举的，当发现某一个产生式产生的终结符和句子的当前结构根本不匹配时，我们就不会再向下继续分析了，因为不管怎么分析也无法得到正确的结果。此时我们就需要回到最近的一次有效的规则，然后继续使用新的规则向后执行，这种行为称为“回溯”。

例如，我们同样取上面的 aab 句子，接下来我们用自顶向下分析算法来判断下面的 CFG 能否推导出句子 aab。

S –> AB
A –> aA | ε
B –> b | bB

第一步：从起始状态 S 开始，产生式只有一个

中间状态	使用的产生式
S	S -> AB
AB

第二步：我们开始对 A 进行展开，可是 A 的展开式有两个。我们分析发现，句子 aab 的开头必须是 a，所以ε这种展开形式就被剔除了，我们选用 aA 这个产生式进行展开

中间状态	使用的产生式
AB	A -> aA
aAB

第三步：我们继续对 A 进行展开，此次展开和第二步使用同样的产生式

中间状态	使用的产生式
aAB	A -> aA
aaAB

第四步：此时我们需要继续对 A 进行展开，此时我们分析发现，这里 A 必须使用 A -> ε

中间状态	使用的产生式
aaAB	A -> ε
aaB

最后，使用 B -> b 即可构建句子 aab，说明句子 aab 是符合该文法的。

中间状态	使用的产生式
aaB	B -> b
aab

我们可以把自顶向下分析算法总结如下：

tokens = []
i = 0
stack = [S] # S 是起始符号
while stack is not None:
    if stack[top] is terminal t:
        if t == tokens[i]:
            i += 1
            pop()
        else
            backtrace()  # 回溯
    else stack[top] is nonterminal T:
        pop()
        push(the next right hand of T)

2. 递归下降分析算法

递归下降分析算法本质也是一种自顶向下分析算法，其基本思想如下：

对每一个非终结符构造一个分析函数
用前看符号指导产生式规则的选择

递归下降分析算法使用“分治法”来提高分析的效率，对于每一个产生式规则，都应该定义一个自己函数。因为在上下文无关文法中，终结符不可能出现在产生式的左边（可以在产生式左边出现终结符的文法叫做上下文有关文法），上下文无关文法中所有的产生式左边只有一个非终结符。所以我们在调用产生式规则的函数后，就分为两种情况：

遇到终结符，因为终结符本质上是 token，所以直接把这个终结符和句子中对应位置的 token 进行比较，判断是否符合即可；符合就继续，不符合就返回
遇到非终结符，此时只需要调用这个非终结符对应的函数即可。在这里函数可能会递归的调用，这也是算法名称的来源。

简单来说，就是遇到非终结符就调用函数，遇到终结符就比较；例如，同样对于文法 G：

S –> AB
A –> aA | ε
B –> b | bB

我们通过递归下降分析来判断 aab 是否符合该文法，算法如下（_parser.py_）：

EOF = '\n'  # 用换行符作为EOF符号

class Parser(object):

    def __init__(self, sentence):
        self.sentence = sentence
        self.current_pos = 0  # 当前的token下标

    def parse_S(self):
        self.parse_A()
        self.parse_B()

    def parse_A(self):
        token = self.get_next_token()   # 从句子中取出一个Token
        if token == 'a':                # 和CFG中的Token进行比较
            self.parse_A()              # 执行非终结符所对应的函数
        elif token != 'a':
            self.put_token_back()

    def parse_B(self):
        token = self.get_next_token()
        if token == 'b':
            token = self.get_next_token()
            if token == EOF:
                pass
            else:
                self.parse_B()
        else:
            raise Exception('非终结符 B 解析异常')

    def get_next_token(self):
        if self.current_pos == len(self.sentence):
            raise Exception('数组越界')

        next_token = self.sentence[self.current_pos]
        self.current_pos += 1
        return next_token

    def put_token_back(self):
        self.current_pos -= 1


if __name__ == '__main__':
    sentence = 'aab'
    parser = Parser(sentence + EOF)
    parser.parse_S()

以上代码只要能正常运行结束而不出现异常，就说明句子’aab’符合此文法。

让我们来分析一下代码中的逻辑：

因为 S 的产生式是非终结符 A 和 B，所以只需要调用 A 和 B 的函数即可
A 产生式涉及到了终结符，所以我们需要先从句子取一个 Token，然后根据 Token 的值进行逻辑判断：如果 token 是 a，则获取到非终结符 A，继续递归执行 A 的函数；如果不是 a，那么不做任何操作，还要把当前的 token 放回到句子中
B 产生式第一个 token 是一样的，无法进行区分，我们可以用第二个 token 判断：如果已经到了句子结尾（也就是说此 token 不是 b），不做任何操作；如果还有 token，则继续执行

3. LL(1) 分析算法

LL(1) 算法也是一个自顶向下的分析算法，它的定义为：从左（L）向右读入一个程序，最左（L）推导，采用一个（1）前看符号。LL(1) 算法和自顶向下分析算法本质上是一致的，它们的区别就在于 LL(1) 算法使用了一种称为分析表的工具来避免了回溯操作，提高了效率。在现实中，我们可以根据某种 LL(1) 分析器来生成分析表，之后根据分析表来进行语法分析操作，我们可以认为这种方法是一种半自动的语法分析方法。LL(1) 的总体工作方式如下所示：

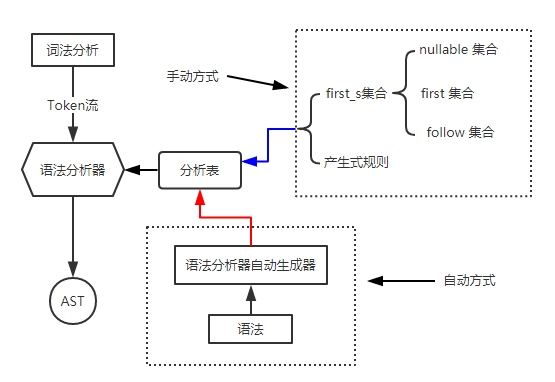
例如对于文法（注意我们这里给每个产生式加上了序号，方便区分）

S → F
S → ( S + F )
F → 1

之后我们根据这个文法来构建一张分析表_（分析表的构建方式会在下面讲到，这里先不做讨论）_如下：

|N\T|（|）|1|+|$|
|:–:|:–:|:–:|:–:|
|S|2|-|1|-|-|
|F|-|-|3|-|-|

有了上面这个分析表之后，我们开始从左向右对句子（例如：( 1 + 1 )）进行分析，它的分析流程如下：

tokens = []
i = 0
stack = [S] # S 是起始符号
while stack is not None:
    if stack[top] is terminal t:
        if t == tokens[i]:
            i += 1
            pop()
        else
           error()
    else stack[top] is nonterminal T:
        pop()
        push(the correct right hand of T)

仔细观察我们就知道这里的流程和自顶向下分析算法的流程的区别就在于 13 行和第 10 行，在第 13 行我们如果能够一次就取到正确的产生式规则而不是使用穷举去猜测，那么算法效率自然可以提高。关键就在于我们要怎么样才能一次性取到正确的产生式，分析表能够帮助我们完成这样的操作。我们详细的执行一次语法分析过程来看分析表是怎么工作的：

最开始栈中的元素为：S；执行 else 中的代码，把 S pop 出去。此时第一个 token 为 (，查阅分析表可得我们应该执行产生式 2，所以被 push 进行 stack 的值为 ( S + F )
此时栈为： ( S + F )；栈顶元素(等于当前的 token，( 被 pop，token 向后移一位
栈：S + F)；当前 token 为 1，栈顶元素 S，查分析表可得产生式 1，栈变为 F + F)
栈：F + F)；栈顶 F，token 1
栈：1 + F)；栈顶 1，token 1
栈：+ F)；栈顶+,token +
栈：F)；栈顶 F，token 1
栈：1)；栈顶 1，token 1
栈：)；栈顶 )，token )
栈：None；token 为空。流程结束

因为以上流程并未报错，所以我们可以推出(1 + 1)可以被此文法描述。至此我们了解到分析表的强大，它避免了回溯操作，大量降低操作时间，提高解析速度。那么问题来了，如此有用的分析表是怎么被构造出来？_（从上面的工作图我们已经知道了分析表可以通过手动和自动两种方式来创建，我们这里的算法原理讲的是 LL(1) 的手动生成分析表的方式，自动方式读者可以查阅相关资料和软件。）_我们需要先了解几个在构造分析表的时候所要用的集合：first 集和 follow 集，以及 nullable 集合。

nullable 集合：
1. 产生式 x -> 空，则 X 属于 nullable 集合；
2. x -> Y1…Yn，Y1 到 Yn 都是非终结符且都属于 nullable 集合，则 X 属于 nullable 集合；

nullable 集合的计算方法：

nullable = {}
while nullable is changing:
    for p: x - > β in productions:  # 遍历所有的产生式
        if β is 空：
            nulable.append(x)
        if β is Y1..Yn:
            if Y1 in nullable and ... and Yn in nullable:
                nulable.append(x)

first 集合：对于产生式 x -> β1…βn，
1. 如果β1 是终结符：first(x) = {β1}
2. β1 是非终结符，first(x) U= first(β1)；
  - 如果β1 属于 nullable，first(x) U= first(β2)；
  - 如果β2 属于 nullable，first(x) U= first(β2)；
  - …

fisrt 集合的计算方法：

for nonterminal n in all_nontermials:
    fisrt(n) = {}  # 初始化所有的first集
while some set is changing:  # 有集合发生了变化
    for p: x - > β1..βn in productions:  # 遍历所有的产生式
        for βi in β1 to βn:
            if βi is terminal:
                first(x).append(βi)
                break
            elif βi is nonterminal:
                first(x).append(first(βi))
                if βi not in nullable:  # 如果βi属于nullable，则还要继续向下计算
                    break

follow 集合：follow（后继）字符集合可以看成所有可以合法的站在此非终结符后面的终结符（可能包括结束符 $ 、但不包括 ε ）的集合。

follow 集合的计算方法：

for nonterminal n in all_nontermials:
    fisrt(n) = {}  # 初始化所有的first集
while some set is changing:  # 有集合发生了变化
    for p: x - > β1..βn in productions:  # 遍历所有的产生式
        tmp = follow(x)  # follow表示跟在x后面的符号集合
        for βi in βn to β1:  # 逆序
            # 下面的所有tmp都代表的是后一个元素的first集合
            if βi is terminal:
                tmp = {βi}  # 作为一个新的follow符
            elif βi is nonterminal:
                follow(βi).append(tmp)  # 把此follow符加入到非终结符的follow集合中
                if βi not in nullable:
                    tmp = first(βi)  # 不为空，则前面一个非终结符的follow集合应为此非终结符的first集合
                else:
                    tmp.append(first(βi))  # first集合为空，无法独立存在了，只能把加上去了

follow 集合存在意义在于如果某个产生式右部的非终结符的 first 集合全都是 ε，则此时取 follow 集。

我们至此已经可以获取到 nullable 集、first 集和 follow 集，现在我们可以根据这几个集合来构建 first_s 集，然后我们可以把 first_s 集合看作是对每一条产生式的计算规则。有了 first_s 集，之后再和产生式结合就可以创建分析表了。first_s 集的生成方式如下：

for p in productions:
    first_s(p) = {}  # 集合初始化为空
# 获取一个产生式的 p 的first_s集
get_first_s(p: N -> β1..βn):
    for βi in β1 to βn:
        if βi is terminal:
            first_s(p).append(βi)
            return
        if βi is nonterminal:  # 非终结符
            first_s(p).append(first(βi))
                if βi not in nullable:
                    return
    first_s(p).append(follow(N)  # 如果全是空，那么会运行到这里，此时把N的follow集加到first_s里面

有了 first_s 集之后，我们就可以构造分析表了。我们把 first_s 集合与产生式结合起来，把 first_s 集合的值作为横坐标，非终结符作为纵坐标，产生式规则作为值，就可以创建出一张分析表了。这里说的创建分析表的方式不免有些抽象，下面我们借助一个例子来完整的看一下一个分析表是怎么被创建出来的。

我们还是使用上面的例子来进行说明，假设我们已经有了一个文法 G：

S → F
S → (S + F)
F → 1

我们想要用此文法生成一个分析表。

首先我们生成 nullable 集合，根据上面的 nullable 集合的生成方式可知，此处的 nullable 集合为空集 {}。
first 集合的计算过程参考上面的计算方式，计算结果如下：

first(F): { 1 }
first(S): { ( } U { 1 } = { (, 1 }  # 取两个的并集

follow 集合根据计算结果为：

follow(S): { +, ) }
follow(F): { ) }

有了 nullable，first 和 follow 集合，我们可以计算出 first_s 集合，这里的序号和产生式中的序号是一一对应的：

1.S -> { 1 }
2.S -> { ( }
3.F -> { 1 }

接着我们用 first_s 集和产生式集合来构建分析表，构建方式很简单。横轴为终结符，纵轴为非终结符，找到对应的产生规则把序号填入表中即可：

N\T	(	)	+	1
S	2	-	-	1
F	-	-	-	3

对比可以发现，这里的分析表和我们上面用来进行句子识别的分析表是一样的，说明我们的构建是正确的。

小结：上面我们讲了 LL(1) 算法的主要内容，需要理解 LL(1) 算法其实就是对于每个非终结符，能够通过查阅分析表找到正确的产生式规则，这种类似于“偷看”的策略能够避免“回溯”操作，可以有效的提高语法分析的效率。

⚠ 需要注意的是，LL(1) 文法不能拥有左递归，否则会导致递归到死，所以如果使用 LL(1) 文法则需要消除左递归。

4. 自底向上分析算法

自底向上分析算法是语法分析的另一类重要算法，它包含了 LR(0) 算法、SLR 算法和 LR(1) 算法。自底向上分析算法的主要方式是根据句子的 Token，使用产生式来自右向左进行分析，即把右侧的内容“收缩”为左侧的非终结符，这种行为我们称为规约（reduce）。

由于精力有限（其实是懒），这里就不对自底向上分析算法做介绍了，想要了解的读者可以自行查阅相关的资料来进行学习。

语法制导翻译

语法制导翻译（Syntax-directed translation，SDT），是在解析（parse）输入的 Token 时，给每一个产生式规则附加一个语义动作（一个代码片段），即把语法“翻译”成一串“动作”，故名“语法制导翻译”。

例如，我们可以在语法动作中加入生成抽象语法树的行为。

分析树和抽象语法树

语法分析不但要判断给定的句子是否符合语法结构，而且还要分析出该句子符合哪些结构，也就是说，要分析出这个句子是怎么从起始符号开始产生出来的，并根据产生过程生成语法树。例如，对于 “我吃饭” 这句话，单纯的知道这句话符合某一个 CFG 是没有意义的，只有我们知道了主语、谓语和宾语分别对应的是那个词，我们才能真正理解这句话的含义。

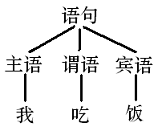
以第一小节的 CFG 为例，我们要从它推导出句子 aab，则推导方式如下：

S => AB => aAB => aaAB => aaB => aab，这个推导过程可以用下面的（语法）分析树来表示：

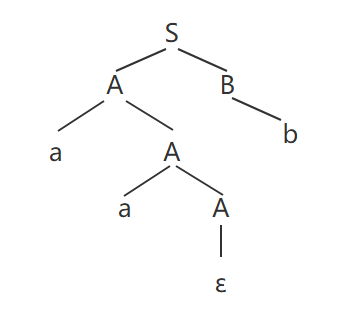
可以去掉此分析树中一些多余的节点，并进一步浓缩，得到抽象语法树（Abstract Syntax Tree, AST）：

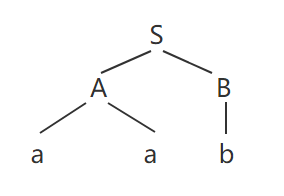
⚠ 需要注意的是，CFG 是可能存在二义性的（歧义），例如下面这个例子。

E -> num | E + E | E * E

上面这个 CFG，对于句子 1 + 2 * 3，它可以生成以下两种 AST：

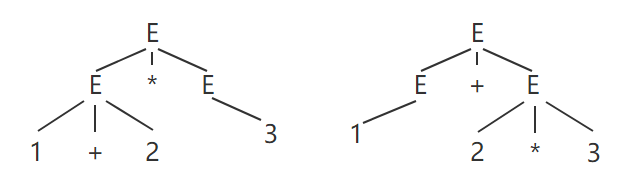
CFG 的二义性将导致同一个程序有多个不同的含义，使得程序的运行结果不唯一。解决二义性的方法就是对文法进行重写，例如把上面的文法改写成如下形式即可。

E -> E + T | T
T -> T * num | num

具体语法和抽象语法：

具体语法是语法分析器使用的语法
抽象语法是用来表达语法结构的内部表示

参考：

http://pandolia.net/tinyc/ch9_context_free_grammar.html
http://pandolia.net/tinyc/ch10_top_down_parse.html

聊聊编译原理（二） - 语法分析