编译器（Compiler），是一种计算机程序，它会将用某种编程语言写成的源代码（原始语言），转换成另一种编程语言（目标语言）。—— 维基百科

把实现编译器过程中所用到的策略与方法总结起来，这就是编译原理，其主要包含了编译器的构造与优化。

一般来说编译器的内部包含了如下的工作步骤：

  1. 词法分析；
  2. 语法分析；
  3. 语义分析；
  4. 生成中间表示（intermediate representation，IR）；
  5. 代码生成；
  6. 优化；

一般来说到生成中间表示这过程中的操作被称为编译器的“前端”，而从IR到最终结果被称为编译器的“后端”。也就是说1 ~ 4步为编译器的前端，而5 ~ 6步为编译器的后端。IR的目的在于保证编译器的跨平台，对于不同的平台，它们的IR表示是一样的，区别只在于代码生成和优化阶段。有了IR，我们在不同平台上编译器的前端就可以复用了，只需要对应不同的平台开发其对应的后端就可以了，减少了工作量。

词法分析

词法分析是编译工作的第一步，它的主要工作是把输入的程序源代码字符流转化为记号（Token）流。例如，对于如下语句，在进行了词法分析操作之后，对应的会生成 int，a，=，0，;这几个记号。

1
int a = 0;

一般来说词法分析的实现主要有两种方式：

  1. 手工编码构造词法分析器，手动构造词法分析器的优点是方便对细节进行控制，缺点是比较复杂且容易出错；
  2. 使用词法分析器的生成器（例如：JavaCC, Yacc, Lex），词法分析器的生成器是一种根据给定的规则把输入构建成Token并输出的程序，其优点时使用简单；

出于学习的目的，我们这里主要讨论手工构造词法分析器的方式；至于词法分析器的生成器的方式，你可以任选一个流行的生成器进行深入了解。

数学工具

词法分析阶段会用到以下几个数学工具：

  • 正则表达式（Regular Expression, RE）
  • 确定性有限状态自动机（DFA）
  • 非确定性有限状态自动机（NFA）

手工构造词法分析器的步骤如下，我们通过RE来实现对Token的描述：

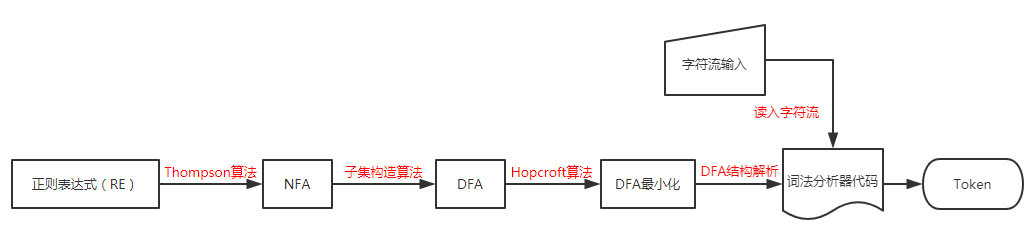
下面我们按照此图中的顺序，了解一下在这几个步骤中所用到的算法以及它们的实现方式。

1. Thompson算法

我们已经知道一个RE可能会包含如下几种情况：

  • ε：代表空；
  • c：代表一个输入字符；
  • e1 e1：两个re的连接关系；
  • e1|e2：两个re的选择关系；
  • e1*：闭包，代表一个re重复0次或多次

例如，对于RE a(b|c)*，我们可以创建如下的NFA：

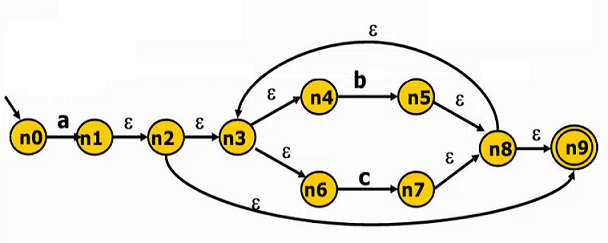
我们发现，RE和NFA的对应关系还是很清晰的，事实上只需要一些简单的递归操作即可以实现从RE到NFA的转换。

2. 子集构造算法

通过不断的构建一个个的状态集合，这些集合都是自动机的所有状态的子集，这就是子集构造算法名字的意义。这种转化算法的本质在于对于每一个状态集合，给该集合一个输入，会得到一个新的状态的集合，通过这种方式来把一个NFA转化为一个DFA。

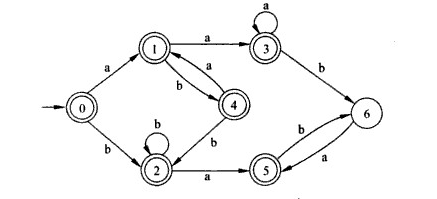
例如下面这个NFA，我们可以先把它状态集合的转移情况列出来，并用一个二维表来表示：

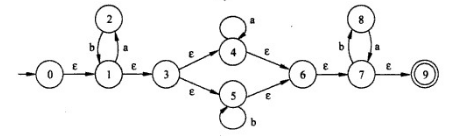
二维表表示集合间的转移关系：

  • 表中的第一列表示不需要任何输入（即输入ε）进行状态转移；
  • 第二列表示了在当前状态的集合下，对于每个状态输入a，之后把得到的状态组合起来作为一个新的集合；
  • 第三列表示对所有状态输入b，得到最终的状态集合；

上表是对所有的状态集进行a和b的输入操作，之后把新得到的状态集再次输入a和b进行转移得到新的状态集，如此反复输入并转移直到最终到达接受状态。

如果把上表的每个状态集合取个别名，例如1、2、3…，那么我们可以把上表改写成如下的形式，这样使得结构更加的清晰，不过集合和别名之间的对应关系需要被保存下来。

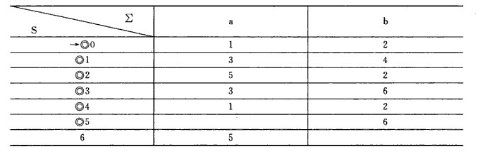
之后，根据上表我们可以的得到这样的一个DFA。至此，NFA到DFA的转化结束。

3. Hopcroft算法

Hopcroft算法是DFA到DFA的转化，其目的是减少DFA的状态和边，对DFA进行简化，这样可以使得后面的操作变得简单。

首先我们需要知道最小状态DFA所需要遵守的规则：

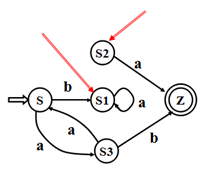
  1. 没有多余状态；

    1. 什么是多余状态？ 从这个状态没有通路到达终态：S1；从开始状态出发，任何输入串也不能到达的那个状态：S2
    2. 如何消除多余状态？ 删除

  2. 没有两个状态是互相等价；互相等价需满足下面两个条件：

    1. 兼容性（一致性）条件——同是终态或同是非终态
    2. 传播性（蔓延性）条件——对于所有输入符号，状态s和状态t必须转换到等价的状态里

DFA最小化分为以下几步，它主要是根据上面的不可互相等价规则来进行操作的：

  1. 把DFA拆分为非接受状态（N）和接受状态（A）这两个集合；
  2. 对于同样的输入，某个集合中的状态产生了不同的结果（这里的结果不同指的是转移状态所处的集合不同），那么根据结果集合的不同应该把这些状态从该集合拆分为新的集合；
  3. 反复进行第2步，直到不可再拆分，此时的集合就可以构成一个新的DFA；

例如，对于如下的DFA，我们对其进行最小化操作。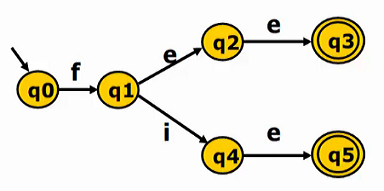

  1. 我们根据N和A对其进行拆分，得到集合N {q0, q1, q2, q4}, A {q3, q5}
  2. 对于集合A，任何输入都不能对它们区分，则它们已不可拆分
  3. 对集合N，我们输入e，q0和q1转移到集合N，q2和q4转移到集合A，则集合N可以拆分为N1 {q0, q1}和 N2 {q2, q4}
  4. 集合N2只接受e且转移结果一致（都是转移到A），其不可再区分
  5. 集合N1输入e，q0转移到N1（因为它还是q0状态），q1转移到N2，则N1可以再被拆为{q0}和{q1}
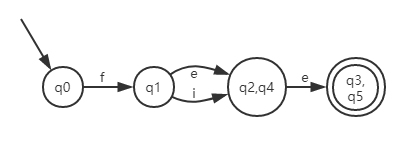
  6. 所有的集合都不可再拆分，现有集合为 {q0}, {q1}, {q2, q4}, {q3, q5} 我们把这些集合生成一个新的DFA，这个新的DFA比初始的6个状态少了两个状态，结构变得简单了。

4. DFA结构解析并生成词法分析器

在上面的我们已经生成了一个符合要求的DFA，现在我们把这个DFA作为输入读入到程序中，然后通过某种方式把这个DFA转化为某种程序易描述的数据结构（例如数组），之后程序利用该结构对输入的字符流（即某种语言的源代码）进行解析。

例如：利用二维数组对DFA结构进行描述，左侧表示当前状态，上方表示输入，框中表示转移结果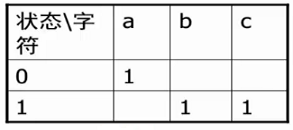

从概念上来说，DFA实际上是一个有向图。我们可以通过转移表、跳转表等代码表示来实现对DFA的识别和Token的解析。

对于识别出来的Token，有些Token只有类型（例如：if），有些Token既有类型又有值（例如：101）。

参考：

  1. 【编译原理】:NFA转变为DFA的子集构造法