堆的一个经典的实现是完全二叉树(complete binary tree)，这样实现的堆称为二叉堆(binary heap)。数据结构中的堆和Java或者C++中的堆没有任何关系，它们是两个完全不同的概念。数据结构中的堆拥有如下两个性质：

  • 任意节点小于（或大于）它的所有后代，最小元（或最大元）在堆的根上；
  • 堆是一颗完全二叉树。

因为二叉堆是一棵完全二叉树，所以和以前使用链表来构建树结构不一样，我们使用数组来构建这棵完全二叉树。数组和完全二叉树的对应关系如下图所示：

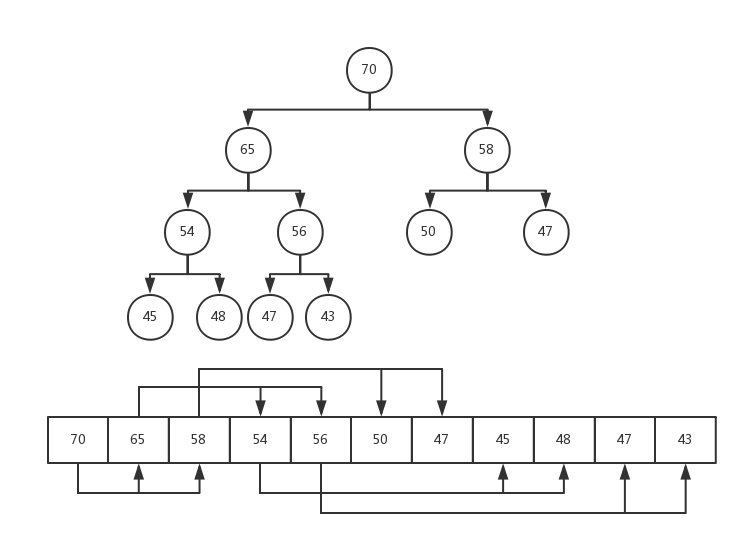
数组和完全二叉树的对应关系

从上图我们可以总结出完全二叉树的数组实现方案中父子节点的关系，假设某个节点的下标为i，则其：

  • 左子节点的下标为2i；
  • 右子节点的下标为2i + 1；
  • 父节点的下标为i / 2；

假设我们使用的是最小元在顶端的二叉堆，那么它的插入和删除操作应该如下来进行：

  • 插入：把待插入的值放在二叉堆的底部，然后把该值和其父亲进行比较，如果小于父亲的值，则进行交换，知道符合规则位置；
  • 删除：删除二叉堆顶端的值，然后把二叉堆的最后一个值放在顶端，之后和其子节点进行比较，如果该节点比两个子节点中小的那一个大，则和该子节点交换，直到该节点比任一子节点都小、或者该节点成为叶节点。

基本概念讲述完毕，下面我看一个Java实现的二叉堆，代码中实现了插入与删除的操作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
import java.util.Arrays;

public class BinaryHeap {

    private int[] heap;

    public BinaryHeap() {
        heap = new int[0];
    }

    public void insert(int num) {
        int length = heap.length;

        int[] newHeap = new int[length + 1];
        System.arraycopy(heap, 0, newHeap, 0, length);
        newHeap[length] = num;
        insertFix(newHeap, length);

        heap = newHeap;
    }

    private void insertFix(int[] newHeap, int last) {
        if (newHeap.length == 1 || last == 0)
            return;
        int parentIndex = (last - 1) / 2;
        if (newHeap[last] < newHeap[parentIndex]) {
            int temp = newHeap[last];
            newHeap[last] = newHeap[parentIndex];
            newHeap[parentIndex] = temp;
            insertFix(newHeap, parentIndex);
        }
    }

    public int removeMin() {
        int removeItem = heap[0];

        int length = heap.length;
        int[] newHeap = new int[length - 1];
        newHeap[0] = heap[length - 1];

        for (int i = 1; i < length - 1; i++) {
            newHeap[i] = heap[i];
        }
        removeFix(newHeap, 0);
        heap = newHeap;
        return removeItem;
    }

    private void removeFix(int[] newHeap, int first) {
        int leftIndex = 2 * (first + 1) - 1;
        int rightIndex = 2 * (first + 1) + 1 - 1;
        if (leftIndex >= newHeap.length || rightIndex >= newHeap.length)
            return;
        int sonIndex;
        if (newHeap[leftIndex] < newHeap[rightIndex])
            sonIndex = leftIndex;
        else
            sonIndex = rightIndex;
        if (newHeap[first] > newHeap[sonIndex]) {
            int temp = newHeap[first];
            newHeap[first] = newHeap[sonIndex];
            newHeap[sonIndex] = temp;
            removeFix(newHeap, sonIndex);
        }
    }

    @Override
    public String toString() {
        return "BinaryHeap [heap=" + Arrays.toString(heap) + "]";
    }

    public static void main(String[] args) {
        BinaryHeap binaryHeap = new BinaryHeap();
        binaryHeap.insert(1);
        binaryHeap.insert(2);
        System.out.println(binaryHeap.removeMin());
        binaryHeap.insert(3);
        binaryHeap.insert(4);
        binaryHeap.insert(0);
        System.out.println(binaryHeap.removeMin());
        System.out.println(binaryHeap);
    }

}

代码本身比较简单，就不多说了，应该很容易就可以看懂。

参考：