本文是计算机的计算系列的第三篇。

1. 图灵机

20 世纪 30 年代，阿兰·图灵（Alan Turing）想要制造出一种可以替代人来进行计算的机器，他在论文《论可计算数及其在判定性问题上的应用》中提出了一种通用的计算机器。具体做法是给一台机器配上一条无限长的空纸带（实际上是一个两端都能随需增长的一维数组），并且允许在纸带上的任意位置读写字符。一条纸带既做存储又做输入：可以在纸带上预先填满字符串当作输入，然后机器在执行过程中可以读取这些字符并在必要的时候覆盖它们。

能访问一条无限长纸带的有限状态自动机叫作图灵机（Turing Machine，TM ）。和下推自动机相比，图灵机不再只被限制在一个栈中，它可以随意的读取纸带上的任意一个位置。不过传统的图灵机并没有使用随意读取纸带任意一个位置的这种方式，而是使用了一个更为简单的方式：

用一个纸带头（tape head）指向纸带的一个特定位置，并且只能在那个位置读取或写入字符。每一步计算之后，纸带头都可以向左或者向右移动一个方格。

这种只进行左移或者右移的操作并没有降低图灵机的计算能力（虽然有些降低了图灵机的执行速度，但是这种牺牲是值得的），却提高了图灵机的简单性。此外，为了进一步保持图灵机的简单，我们在纸带上只会写两个数：0和1。

现在我们已经了解了图灵机的构造及所包含的基本操作了，下面我们开始了解图灵机的转移规则，下面是一组转移规则的示例：

当前状态 读入当前格子的数 写数字到当前的格子 转移到的状态 纸带头移动方向
1 1 0 2 R
1 0 1 3 L

上面是个非常简单的转移规则的例子，第一条是当前状态为1，读入为1，此时向格子上写入0，然后进入状态2，接着纸带头右移；第二条则是当前状态为1，读入为0，此时向个格子上写入1，然后进入状态3，接着纸带头左移。

转移规则还是很容易理解，需要注意的是图灵机把状态机的输入和纸带中的数据联系了起来。想想在下推自动机中，自动机的输入和栈中的数据是割裂开来的，但是在图灵机中，自动机中的输入就是纸带上的数据，这种联系使得图灵机更加简单，因为我们此时只需要考虑纸带就可以，而不再去考虑一个额外的输入了。

其实这种方式有着一个更为重要的优点，也就是我们可以在上一步的转移操作中为下一步的转移操作设计好一个输入，这在下推自动机中是做不到的，因为下推自动机的输入只能由我们人类来给出，而不能由机器给出。我们为图灵机设计好一个最初始的输入和转移规则之后，图灵机可以通过自己给自己设计输入然后永远的执行下去。

同样,我们可以使用示意图来模拟一个图灵机，例如下面这个就代表了一个图灵机，它对应的规则在后面给出了。

图灵机

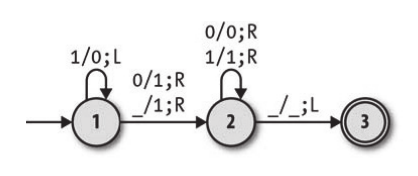
  • 处于状态 1 并且读入一个 0 时，写入一个 1，右移，然后进入状态 2；
  • 处于状态 1 并且读入一个 1 时，写入一个 0，左移，然后保持在状态 1；
  • 处于状态 1 并且读到一个空白时，写入一个 1，右移，然后进入状态 2；
  • 处于状态 2 并且读到一个 0 时，写入一个 0，右移，然后保持在状态 2；
  • 处于状态 2 并且读入一个 1 时，写入一个 1，右移，然后保持在状态 2；
  • 处于状态 2 并且读到一个空白时，写入一个空白，左移，然后进入状态 3。

到这里我们已经大致的了解了图灵机的基本构造。同样的，图灵机也分为确定型图灵机和非确定型图灵机，下面我们将分别进行讨论。

2. 确定型图灵机

确定型图灵机意味着该图灵机的转移规则不会存在冲突，同时也意味着不会有转移规则的缺失问题。对于第二点，因为较为复杂，所以我们和前面一样不予考虑，我们目前只对唯一性进行限制。下面是一个用Python所模拟的图灵机：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
"""
能访问一条无限长纸带的有限状态自动机叫作图灵机（Turing Machine，TM ）
"""


# 纸带
class Tape(object):
    def __init__(self, left, middle, right, blank):
        self.left = left
        self.middle = middle
        self.right = right
        self.blank = blank

    # 纸带头写当前位置
    def write(self, character):
        return Tape(self.left, character, self.right, self.blank)

    # 纸带头左移
    def move_head_left(self):
        # 让纸带可以自动扩展
        if len(self.left) == 0:
            self.left = ['_']
        # -1 在右边的时候是不被包含的
        return Tape(self.left[:-1], self.left[-1], [self.middle] + self.right, self.blank)

    # 纸带头右移
    def move_head_right(self):
        # 让纸带可以自动扩展
        if len(self.right) == 0:
            self.right = ['_']
        return Tape(self.left + [self.middle], self.right[0], self.right[1:], self.blank)

    def __str__(self):
        # 最后一个是空白字符的代表
        return str(self.left + ['[' + self.middle + ']'] + self.right + ['<' + self.blank + '>'])


tape1 = Tape(['1', '0', '1'], '1', [], '_')


# print(tape1)
# tape1 = tape1.move_head_left()
# print(tape1)
# tape1 = tape1.write('0')
# print(tape1)
# tape1 = tape1.move_head_right()
# print(tape1)
# tape1 = tape1.write('0')
# print(tape1)
# tape1 = tape1.write('1')
# print(tape1)


# 和前面的一样，一个图灵机的配置是一个状态和一条纸带的组合
class TMConfiguration(object):
    def __init__(self, state, tape):
        self.state = state
        self.tape = tape

    def __str__(self):
        return str(self.state) + ' -> ' + str(self.tape)


# 图灵机的一个转移规则
class TMRule(object):
    # 参数：当前状态，读入纸带，下一个状态，写入纸带，纸带头移动方向
    def __init__(self, state, read_character, next_state, write_character, direction):
        self.state = state
        self.read_character = read_character
        self.next_state = next_state
        self.write_character = write_character
        self.direction = direction

    # 当一个配置的状态和它当前的读入字符与某一个转移规则的状态和读入字符相等时，
    # 我们可以认为此配置符合该转移规则
    def applies_to(self, configuration):
        return self.state == configuration.state and self.read_character == configuration.tape.middle

    # 根据当前规则，计算出当前配置的下一个配置（注：当前配置必须是已经符合当前转移规则的一个配置）
    def follow(self, configuration):
        return TMConfiguration(self.next_state, self.__next_tape(configuration))

    # 计算出纸带的下一个状态
    def __next_tape(self, configuration):
        written_tape = configuration.tape.write(self.write_character)
        if self.direction == 'L':
            return written_tape.move_head_left()
        elif self.direction == 'R':
            return written_tape.move_head_right()


rule1 = TMRule(1, '0', 2, '1', 'R')
print(rule1.applies_to(TMConfiguration(1, Tape([], '0', [], '_'))))
print(rule1.applies_to(TMConfiguration(1, Tape([], '1', [], '_'))))
print(rule1.applies_to(TMConfiguration(2, Tape([], '0', [], '_'))))
print(rule1.follow(TMConfiguration(1, Tape([''], '0', [''], '_'))))


# 把一个图灵机的规则整理起来就是一个转移规则集合了
class DTMRulebook(object):
    def __init__(self, rules):
        self.rules = rules

    # 根据当前配置找到下一个配置
    def next_configuration(self, configuration):
        return self.__rule_for(configuration).follow(configuration)

    # 根据当前配置去规则集合中找符合要求的转移规则
    def __rule_for(self, configuration):
        for rule in self.rules:
            if rule.applies_to(configuration):
                return rule
        raise Exception("找不到可供使用的规则 ...")


rulebook1 = DTMRulebook([
    TMRule(1, '0', 2, '1', 'R'),
    TMRule(1, '1', 1, '0', 'L'),
    TMRule(1, '_', 2, '1', 'R'),
    TMRule(2, '0', 2, '0', 'R'),
    TMRule(2, '1', 2, '1', 'R'),
    TMRule(2, '_', 3, '_', 'L')
])
configuration1 = TMConfiguration(1, tape1)
print(configuration1)
configuration1 = rulebook1.next_configuration(configuration1)
print(configuration1)
configuration1 = rulebook1.next_configuration(configuration1)
print(configuration1)
configuration1 = rulebook1.next_configuration(configuration1)
print(configuration1)


# 对上面的图灵机进行一些封装
class DTM(object):
    def __init__(self, current_configuration, accept_states, rulebook):
        self.current_configuration = current_configuration
        self.accept_states = accept_states
        self.rulebook = rulebook

    # 判断当前配置是否是可接受的
    def accepting(self):
        return self.current_configuration.state in self.accept_states

    # 转移到下一个配置
    def step(self):
        self.current_configuration = self.rulebook.next_configuration(self.current_configuration)

    # 不断的把配置转移到下一个直到处于接受状态
    def run(self):
        while not self.accepting():
            self.step()
        # 直接可以接受时才返回当前的配置
        return self.current_configuration


dtm = DTM(TMConfiguration(1, tape1), [3], rulebook1)
print(dtm.current_configuration)
print(dtm.accepting())
print(dtm.step)
print(dtm.current_configuration)
print(dtm.accepting())
print(dtm.run())
print(dtm.current_configuration)
print(dtm.accepting())

阅读完并理解以上代码之后你就会发现，图灵机相比于下推自动机要容易理解一点，因为“简单性”也是图灵机的重要性质之一。阿兰·图灵设计这种机器的时候特意让它们保持简单以便容易构建和推导，所以图灵机更容易被模拟出来。

3. 非确定型图灵机

对于一台图灵机，“不确定性”意味着每个状态和字符的组合会允许多于一个的规则，因此从一个起始配置开始会有多个可能的执行路径，这就是我们所说的非确定型图灵机。

和NFA与DFA的关系一样，任意一台非确定型图灵机都可以用一台DTM（Deterministic Turing Machine，确定型图灵机）表示出来，所以我们说：

非确定型图灵机并不能比DTM拥有更大的计算能力

事实上，确定型图灵机代表了从有限计算机器到全能机器的临界点。也就是说，通过升级图灵机规范以使其更强大的任何尝试都注定失败。《计算的本质》中作者还举出了其他的一些计算模型，然而这些模型无一例外地都和图灵机的计算能力等价，因此邱奇、图灵和哥德尔提出了著名的邱奇-图灵论题：

一切直觉上能计算的函数都可用图灵机计算，反之亦然。

4. 通用图灵机

通过把Tape、TMRule、DTMRulebook以及DTM重新实现成图灵机的规则，我们能设计一台图灵机，它能通过从纸带读取其规则、接受状态以及起始配置然后单步执行，模拟任何其他确定型图灵机，本质上这扮演着图灵机规则手册解释器的角色。完成这种工作的机器叫作通用图灵机（Universal Turing Machine，UTM） 。

这里需要理解的是，通用图灵机本身也是一台确定型图灵机，只是这台图灵机能够在内部模拟出其它的图灵机，正是因为其可以模拟出其它的图灵机，所以它的规则就不再是硬编码的。我们使用这台通用图灵机的时候，可以根据需要来模拟一台不同的图灵机，而这台新的图灵机的转移规则可以在模拟的时候进行规定，所以此时这台通用图灵机的操作就不再是硬编码的了，而是可以根据需要来进行创建。

5. 从图灵机到CPU

我假设你已经明白了类似于半加器、全加器这样的计算电路，这种电路被称之为组合逻辑电路。它的任一时刻的稳态输出，仅仅与该时刻的输入变量的取值有关，而与该时刻以前的输入变量取值无关。

与组合逻辑电路相对应的时序逻辑电路，时序逻辑电路是指电路任何时刻的稳态输出不仅取决于当前的输入，还与前一时刻输入形成的状态有关。看到了时序逻辑电路，是不觉得它和自动机的性质非常相似？事实上，给定任何确定自动机，我们都可以设计这样一个时序电路。所以我们可以根据通用图灵机的性质来设计一个时序电路，而这样的一个电路，就是CPU。

但是需要注意的是，CPU不一定非要是由电路构成，因为通用图灵机本身是一个抽象的模型，所以我们自然可以通过各种来实现这个抽象模型。事实上，第一个把计算和电子元件联系起来的人是香农，他在论文《对继电器和开关电路中的符号分析》中首次提出通过电器元件来进行数学计算，并证明了可以通过继电器电路来实现布尔代数的逻辑运算。

现代CPU的执行流程主要包括如下几步（CSAPP 4.3.1节）：

  1. 取指（fetch）
  2. 译码（decode）
  3. 执行（execute）
  4. 访存（memory）
  5. 写回（write back）
  6. 更新PC（PC update）

这几个步骤大致相当于图灵机的：

  1. 读纸带
  2. 寻找对应的转移规则
  3. 找到规则，执行
  4. 向纸带上写回数据
  5. 更新状态
  6. 读写头向左或向右移动

下面可以通过一个表格来进行更直观的对比：

CPU 图灵机
取指 读纸带
译码 寻找对应的转移规则
执行 找到规则，执行
访存 向纸带上写回数据
写回 （同上）
更新PC 更新状态，读写头向左或向右移动

我们可以发现图灵机和CPU的执行过程十分相似，因为CPU本来就是根据图灵的计算模型而设计出来的。

到这里图灵机就讲的差不多了，这里有一篇文章也是讲图灵机的，算是一篇科普文，讲的也是比较不错的，有兴趣的可以看看。