计算机的计算（二） - 下推自动机

本文是计算机的计算系列的第二篇。

1. 下推自动机

自带栈的有限状态机叫作下推自动机（PushDown Automaton，PDA）。

上面给出了下推自动机的概念，那么为什么我们要在有限自动机的基础上给其增加一个栈来构建下推自动机呢？其根本原因在于有限状态机本身无法存储数据，而加上了栈之后的下推自动机则具有了数据存储能力。具有了存储能力之后，下推自动机的计算能力相较于有限自动机得到了进一步的增强。

我们已经知道，有限自动机在进行状态转移的时候，需要读取一个输入，然后根据当前状态已经输入来进行状态转移。下推自动机在进行状态转移的时候同样要依赖于当前状态和输入，不过，因为下推自动机有了栈的概念，所以在进行状态转移的时候我们还需要一点别的东西——读栈和写栈操作。例如下图这样的一个下推自动机：

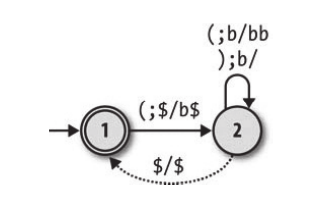
我们可以把这个下推自动机用这样的转移列表列出来，注意这里的 $ 符号，因为栈为空的状态并不是很好判断，所以我们添加了这个字符来代表栈为空，也就是说栈的最底部永远应该保持有 $ 这个字符。最下面的虚线代表着当栈为空且状态为2时（我们使用虚线来代表不需要有输入的转移情形，即自由移动），此时不需要任何输入，栈会自动的弹出 $ 然后再压入 $，随后状态从2变为1。

当前状态	输入字符	转移状态	栈顶字符（读入/弹出）	压入字符
1	(	2	$	b$
2	(	2	b	bb
2	)	2	b	不压入
2	无输入	1	$	$

相对于有限自动机，下推自动机只是增加了一个入栈和出栈的操作，可以说并不复杂，但是需要提醒的一点是：对于下推自动机，栈顶的元素也是转移的规则之一。怎么理解这句话呢？下面我通过一个小例子来说明。

有如下两个转移规则

当前状态	输入字符	转移状态	栈顶字符（读入/弹出）	压入字符
1	a	2	x	$
1	a	3	y	$

当在状态1读到输入a的时候，此时并不能决定到底要转移到那一个状态，而是要根据此时的栈顶元素（x或是y）来判断要进行哪一种的转移操作，所以说栈顶元素也是转移的规则之一。《计算的本质》中是这样描述这个特性的：

在某种程度上，下推自动机还能控制自己。在规则和栈之间有一个反馈环——栈的内容影响机器应该遵守的规则，而按照某个规则执行也会影响栈的内容——这允许PDA在栈中存储一些信息，这些信息可以影响它将来的执行。

因为下推自动机是有限自动机的扩充，所以下推自动机也分为确定性下推自动机和非确定性下推自动机，下面将会详细介绍。

2. 确定性下推自动机

什么是确定性？即 无冲突、无遗漏。

• 对于无冲突，我们只要保证下推自动机在进行状态转移的时候不会产生模棱两可的规则即可；
• 而无遗漏这个要求操作起来就比较的棘手，因为下推自动机一般很难把所有的转移规则都覆盖到，所以一般的做法是忽略这个约束并允许DPDA（确定性下推自动机，Deterministic PushDown Automaton）只定义完成工作所需的规则，并且假定一台DPDA在没有规则可用时将进入停滞状态。

了解DPDA的定义后，就开始使用Python来模拟一个下推自动机吧，代码实现如下：

"""
确定性下推自动机，Deterministic PushDown Automaton
"""


# 定义一个栈
class Stack(object):
    # 初始时栈底的元素
    def __init__(self, init):
        self.__storage = init

    def top(self):
        return self.__storage[-1]

    def push(self, p):
        # 压入的内容做遍历，靠近后面的内容应该先被压入
        for i in reversed(p):
            self.__storage.append(i)

    def pop(self):
        return self.__storage.pop()


# 名词[配置]表示一个状态和一个栈的组合，其实上相当于以前的[一个状态]
# 为什么要定义[配置]呢？目的在于把状态和栈这两种元素组合起来形成一个整体，方便使用
class PDAConfiguration(object):
    def __init__(self, state, stack):
        self.state = state
        self.stack = stack


# DDPA的转移规则
class PDARule(object):
    # 参数：当前状态，输入，下一个状态，（栈）弹出字符，压入字符
    def __init__(self, state, character, next_state, pop_character, push_characters):
        self.state = state
        self.character = character
        self.next_state = next_state
        self.pop_character = pop_character
        self.push_characters = push_characters

    # 下一个配置：1. 下一个状态就是 next_state 参数，2. 下一个配置的栈由方法 next_stack 根据当前的栈信息算出
    def follow(self, configuration):
        return PDAConfiguration(self.next_state, self.__next_stack(configuration.stack))

    # 判断指定配置执行指定输入时是否可用当前的转移规则
    def applies_to(self, configuration, character):
        return self.state == configuration.state \
               and self.pop_character == configuration.stack.top() and self.character == character

    # 下一个栈的计算，先弹出再压入即可
    def __next_stack(self, stack):
        stack.pop()  # 弹出
        stack.push(self.push_characters)  # 压入
        return stack


# 转移规则集合
class DPDARulebook(object):
    def __init__(self, rule_set):
        self.ruleSet = rule_set

    # 用于获取下一个配置
    def next_configuration(self, configuration, character):
        return self.__rule_for(configuration, character).follow(configuration)

    # 根据当前的配置和输入来查找对应的转移规则
    def __rule_for(self, configuration, character):
        for rule in self.ruleSet:
            if rule.applies_to(configuration, character):
                return rule
        raise Exception("找不到可供使用的规则 ...")


rulebook = DPDARulebook([
    PDARule(1, '(', 2, '$', ['b', '$']),
    PDARule(2, '(', 2, 'b', ['b', 'b']),
    PDARule(2, ')', 2, 'b', []),
    PDARule(2, None, 1, '$', ['$'])
])


class DPDA(object):
    # 参数：初始配置，接受状态，规则集合
    def __init__(self, current_configuration, accept_states, rule_book):
        self.current_configuration = current_configuration
        self.accept_states = accept_states
        self.rule_book = rule_book

    # 判断当前的状态是否是接受状态
    def accepting(self):
        return self.current_configuration.state in self.accept_states

    # 输入
    def read_character(self, character):
        self.current_configuration = self.rule_book.next_configuration(self.current_configuration, character)

    # 同样为了简化操作，方便连续输入
    def read_string(self, string):
        for c in string:
            self.current_configuration = self.rule_book.next_configuration(self.current_configuration, c)


if __name__ == '__main__':
    dpda = DPDA(PDAConfiguration(1, Stack(['$'])), [1], rulebook)
    print(dpda.accepting())
    dpda.read_string('(()')
    print(dpda.accepting())

虽然代码的实现看上去挺复杂的，但是我们只需要牢记两点：

1. 下推自动机只是有限自动机增加了一个栈而已，所以我们只是增加了栈的压入和弹出操作
2. 下推自动机的转移规则还需要指定栈顶元素，栈顶元素不一样的不能算为同样的转移规则

3. 非确定性下推自动机

在介绍非确定性下推自动机之前，我们写来了解一下使用非确定性下推自动机有什么好处。观察下面这张图，这是一个用来检测一个输入是否是回文的确定性下推自动机。

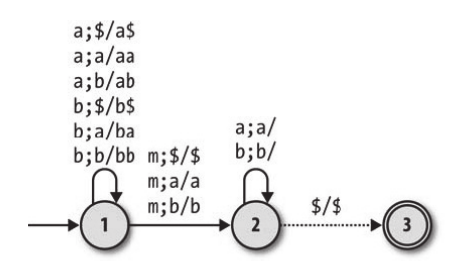
1. 处于状态1且输入了a或者b的时候，每输入一个输入就会在栈顶把这个输入加上去（和之前不一样，我们在这里把直接把输入入栈了，也就是把输入和栈联系了起来。在之前，输入和栈内元素我们都是区分开来的）；
2. 在输入了 m 之后，又会把栈内元素根据输入顺序弹出来（也就是当栈顶为a时，我们必须输入a，之后a被弹出，下一个元素继续进行同样的操作）。

在有了这种机器之后，我们就能识别出类似于 babbamabbab 这样的回文了。但是我们还需要一个额外的 m 来进行分割的操作，这样感觉并不是很优美。我们可以使用非确定性下推自动机来完成同样的操作（出于简单考虑，该自动机只支持偶数个字母的判断）：

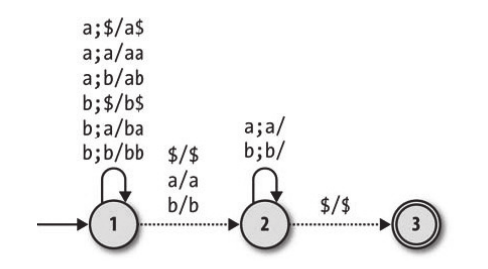
上面这个机器除了状态1到状态2的转移操作和之前的DPDA不一样，其余完全一样。也就是说从状态1到状态2的转移不需要任何的确定性的约束，这种没有确定性约束的下推自动机叫作非确定性下推自动机。下面就是一个非确定性下推自动机的模拟：

"""
非确定性下推自动机
"""


# 定义一个栈
class Stack(object):
    # 初始时栈底的元素
    def __init__(self, init):
        self.__storage = init

    def top(self):
        return self.__storage[-1]

    def push(self, p):
        # 压入的内容做遍历，靠近后面的内容应该先被压入
        for i in reversed(p):
            self.__storage.append(i)

    def pop(self):
        return self.__storage.pop()

    # 相当于 Java 的 toString 方法
    def __str__(self):
        return str(self.__storage)


# 名词[配置]表示一个状态和一个栈的组合，其实上相当于以前的[一个状态]
# 为什么要定义[配置]呢？目的在于把状态和栈这两种元素组合起来形成一个整体，方便使用
class PDAConfiguration(object):
    def __init__(self, state, stack):
        self.state = state
        self.stack = stack

    def __str__(self):
        return str(self.state) + ':' + str(self.stack)


# DDPA的转移规则
class PDARule(object):
    # 参数：当前状态，输入，下一个状态，（栈）弹出字符，压入字符
    def __init__(self, state, character, next_state, pop_character, push_characters):
        self.state = state
        self.character = character
        self.next_state = next_state
        self.pop_character = pop_character
        self.push_characters = push_characters

    # 下一个配置：1. 下一个状态就是 next_state 参数，2. 下一个配置的栈由方法 next_stack 根据当前的栈信息算出
    def follow(self, configuration):
        return PDAConfiguration(self.next_state, self.__next_stack(configuration.stack))

    # 判断指定配置执行指定输入时是否可用当前的转移规则
    def applies_to(self, configuration, character):
        return self.state == configuration.state \
               and self.pop_character == configuration.stack.top() and self.character == character

    # 下一个栈的计算，先弹出再压入即可
    def __next_stack(self, stack):
        stack.pop()  # 弹出
        stack.push(self.push_characters)  # 压入
        # print(stack)
        return stack


"""
↑↑↑ 上面内容和 DPDA 完全一样 ↑↑↑
"""


# 非确定性下推自动机转移规则集合
class NPDARulebook(object):
    def __init__(self, rule_set):
        self.ruleSet = rule_set

    # 用于获取下面的多个配置
    def next_configurations(self, configuration, character):
        configurations = []
        for config in configuration:
            rules = self.__rules_for(config, character)
            for rule in rules:
                configurations.append(rule.follow(config))
        return configurations

    # 根据当前的[配置]和[输入]来查找对应的转移规则
    # 与 DPDA 不同，这里可能会对应多个不同的转移规则，我们用集合来存放这些转移规则
    def __rules_for(self, configuration, character):
        rules = []
        for rule in self.ruleSet:
            if rule.applies_to(configuration, character):
                rules.append(rule)
        return rules


rulebook = NPDARulebook([
    PDARule(1, 'a', 1, '$', ['a', '$']),
    PDARule(1, 'a', 1, 'a', ['a', 'a']),
    PDARule(1, 'a', 1, 'b', ['a', 'b']),
    PDARule(1, 'b', 1, '$', ['b', '$']),
    PDARule(1, 'b', 1, 'a', ['b', 'a']),
    PDARule(1, 'b', 1, 'b', ['b', 'b']),
    PDARule(1, None, 2, '$', ['$']),
    PDARule(1, None, 2, 'a', ['a']),
    PDARule(1, None, 2, 'b', ['b']),
    PDARule(2, 'a', 2, 'a', []),
    PDARule(2, 'b', 2, 'b', []),
    PDARule(2, None, 3, '$', ['$'])
])


class NPDA(object):
    # 参数：初始配置，接受状态，规则集合
    def __init__(self, current_configuration, accept_states, rule_book):
        self.current_configuration = [current_configuration]
        self.accept_states = accept_states
        self.rule_book = rule_book

    # 判断当前的状态是否是接受状态
    def accepting(self):
        for current_config in self.current_configuration:
            if current_config.state in self.accept_states:
                return True
        return False

    # 输入
    def read_character(self, character):
        for i in self.current_configuration:
            print(i)
        # 转移到下一个配置
        self.current_configuration = self.rule_book.next_configurations(self.current_configuration, character)

    # 同样为了简化操作，方便连续输入
    def read_string(self, string):
        for c in string:
            self.read_character(c)


if __name__ == '__main__':
    dpda = NPDA(PDAConfiguration(1, Stack(['$'])), [3], rulebook)
    print(dpda.accepting())
    dpda.read_string('babba')
    dpda.read_character(None)
    dpda.read_string('abbab')
    dpda.read_character(None)
    print(dpda.accepting())

我们同样使用集合来保存非确定性下推自动机的配置的可能情况，具体的思想可以参考DFA到NFA的转化方式。

4. 不等价

我们已经了解了任意的一个NFA都可以转化为一个与其等价的DFA，那么任意一个NPDA都可以转化为一个与其等价的DPDA吗？非常遗憾，答案是否定的。

所以不幸的是，我们的 NPDA 模拟的行为并不像一台 DPDA，也不存在 NDPA 到 DPDA
的算法。无标记的回文问题就是这样一个例子，NPDA 能完成这个问题，但 DPDA 不能，
因此非确定性下推自动机确实比确定性的能力要强。