本文是计算机的计算系列的第一篇。

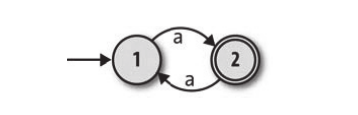
1. 有限自动机

有限自动机（finite automaton），也叫有限状态机（finite state machine），是一台极简的计算机模型。下面是一个非常简单的有限自动机：
简单的有限自动机

  • a被称之为输入；
  • 圆圈1和2我们称之为状态，其中1为起始状态，2为接受状态；
  • 在状态1的时候输入了a，此时会转移到状态2，这种转移我们可以称之为转移规则；
  • 如果一系列的输入能够使得一台有限自动机最终处于接受状态，那么这个输入是可以被这台有限自动机接受的，这个输入的内容可以称之为这台有限自动机的正则语言；否则，这种输入就是被该有限自动机拒绝的；

下面是一台稍微复杂点的有限自动机，对照上面的概念，自己看看能不能理解这些概念：

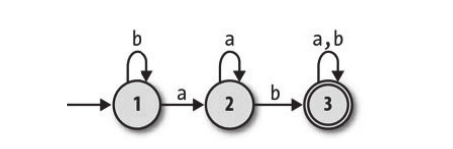
如上所示：

  1. 这台有限自动机一共有1、2、3三种状态，其中1是输入状态，3是接受状态；
  2. 一共有两种输入，即a和b；
  3. 转移规则如下表所示：
当前状态 输入 目标状态
1 a 2
1 b 1
2 a 2
2 b 3
3 a 3
3 b 3

怎么样，很简单吧。OK，我们已经理解了有限自动机的概念了，接下来我们聊聊有限自动机下的两个不同类型：确定性有限自动机和非确定性有限自动机。

2. 确定性有限自动机

具有以下这两个性质的有限自动机可以称为确定性有限自动机：

  • 没有冲突：一个状态对于同样的输入，不能有多个规则，即每个输入只能有一个转移规则；
  • 没有遗漏：每个状态都必须针对每个可能的输入字符有至少一个规则；

说的通俗点就是一个状态对应一个输入只会有一个转移规则；而每个状态都必须包含有所有输入的转移规则，不可以有遗漏；这就是确定性有限自动机。

理解了什么是确定性有限自动机了，接下来就让我们用代码来实现它：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
"""
DFA，确定性有限自动机
"""


# 定义了一个转移规则
class FARule(object):
    # 初始化
    def __init__(self, state, character, next_state):
        self.state = state
        self.character = character
        self.nextState = next_state

    # 通过判断当前的状态和输入和此规则是否相等来决定是否应该使用该种规则
    def applies(self, state, character):
        return self.state == state and self.character == character

    # 获取下一个规则
    def next_state(self):
        return self.nextState


# 如果上面的类是一个转移规则，那么这里就是存储了一个有限自动机的转移规则的集合
class FARuleBook(object):
    def __init__(self, rule_set):
        self.ruleSet = rule_set

    def rules(self):
        return self.ruleSet


# 初始化一个有限自动机的规则集合
rulebook = FARuleBook([
    FARule(1, 'a', 2),
    FARule(1, 'b', 1),
    FARule(2, 'a', 2),
    FARule(2, 'b', 1)
])


# 定义一个确定性有限自动机
class DFA(object):
    # 初始化有限自动机时包含了初始状态、接受状态和转移规则的集合
    def __init__(self, current_state, accept_state, rule_book):
        self.currentState = current_state
        self.acceptState = accept_state
        self.ruleBook = rule_book.rules()

    # 当输入一个字符时，根据当前状态和输入去转移规则中寻找对应的转移规则，
    # 根据规则获取下一个状态，并把下一个状态置为当前状态
    def input_character(self, character):
        for r in self.ruleBook:
            if r.applies(self.currentState, character):
                self.currentState = r.next_state()

    # 根据当前状态来判断是否是输入状态
    def is_accept(self):
        return self.currentState == self.acceptState

    # 为了方便操作，同时也提供了一个可以输入字符串的方法
    def input_string(self, string):
        for c in string:
            self.input_character(c)


# 初始化一个DFA
dfa = DFA(1, 2, rulebook)
# 读入字符串
dfa.input_string('aaaaaaaaaaaaaaaaaaab')
# 判断当前是否处于接受状态
print(dfa.is_accept())

上面就是一个用Python模拟的DFA了，很简单吧。

3. 非确定性有限自动机

所谓非确定性有限自动机（NFA），就是没有了DFA那两条限制的机器，即：

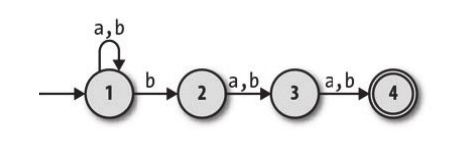
  • 对于某一个状态，读入某一个输入的时候，可能会有多种转移规则；
  • 对于某一个状态，它可能会缺少对应某种输入的转移规则；

说的再多不如示意图来的直观，下面就是一个NFA：
NFA

通过观察上图可以发现，在状态1输入b的时候，可能跳转到状态1，也可能跳转到状态2；而状态4则对任何输入不会有转移。这样的机器就是NFA。

OK，了解NFA的定义之后我们同样可以用Python来对其进行模拟。因为NFA的状态转移可能会对应多种的转移结果，所以与确定性有限自动机不一样，在非确定性有限自动机中我们用一个集合来保存所有可能转移到的状态。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
"""
NFA，非确定性有限自动机
"""


# 定义了一个转移规则
class FARule(object):
    # 初始化
    def __init__(self, state, character, next_state):
        self.state = state
        self.character = character
        self.nextState = next_state

    # 通过判断当前的状态和输入和此规则是否相等来决定是否应该使用该种规则
    def applies(self, state, character):
        return self.state == state and self.character == character

    # 获取下一个规则
    def next_state(self):
        return self.nextState


# 同样，我们需要一个规则转移的集合
class FARuleBook(object):
    # 传入一个规则集合
    def __init__(self, rule_set):
        self.ruleSet = rule_set

    # 通过当前的状态集合和输入，根据转移规则集合，计算出所有可能的输出状态
    def get_next_states(self, current_states, character):
        next_states = []
        rule_set = self.ruleSet
        for current_state in current_states:
            for rule in rule_set:
                if rule.applies(current_state, character):
                    next_states.append(rule.next_state())
        # 使用 set 有助于去除重复的集合
        return set(next_states)


# 初始化一个NFA的规则集合
rulebook = FARuleBook([
    FARule(1, 'a', 1),
    FARule(1, 'b', 1),
    FARule(1, 'b', 2),
    FARule(2, 'a', 3),
    FARule(2, 'b', 3),
    FARule(3, 'a', 4),
    FARule(3, 'b', 4)
])


# 非确定性有限自动机
class NFA(object):
    # 初始化包括初始状态、接受状态、规则转移集合
    def __init__(self, current_state, accept_state, rule_book):
        self.current_state = current_state
        self.accept_state = accept_state
        self.rule_book = rule_book

    # 通过判断接受状态是否处于当前状态之中来测试当前是否可能处于接受状态
    def applies(self):
        return self.accept_state in self.current_state

    # 读入一个输入，根据当前状态获取到所有的可能的输出状态的集合
    def read_character(self, character):
        self.current_state = self.rule_book.get_next_states(self.current_state, character)

    # 同理，制作一个方便读入字符串的方法
    def read_string(self, string):
        for c in string:
            self.read_character(c)


# 创建一个NFA，切记输入状态应该是一个集合
nfa = NFA([1], 4, rulebook)
# 读入 bbb
nfa.read_string('bbb')
# 判断输入是否可能被接受（即输入是否是该有限自动机的正则语言）
print(nfa.applies())

如果你看懂了上面程序，其实上面的代码所模拟的就是上面图例中的NFA。

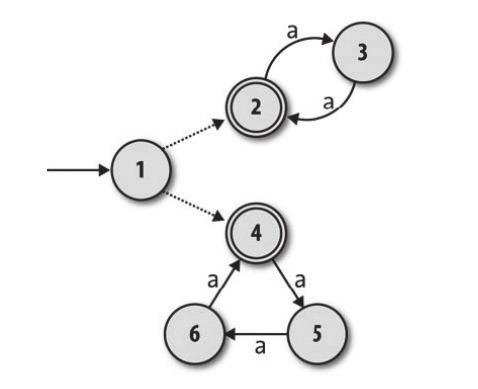
需要注意的是，NFA有一点和DFA极其不一样的地方就在于NFA存在着一种名为自由移动的操作，所谓自由移动也就是说在NFA中某一种状态可以自由的转移到另一个状态而不需要任何的输入，下图就是一个例子：

从状态1到状态2或者状态4的转移操作就叫做自由移动，不需要任何的输入就可以完成状态转移的操作。如果想用代码来描述的话，方式如下：

1
2
FARule(1, None, 2)
FARule(1, None, 4)

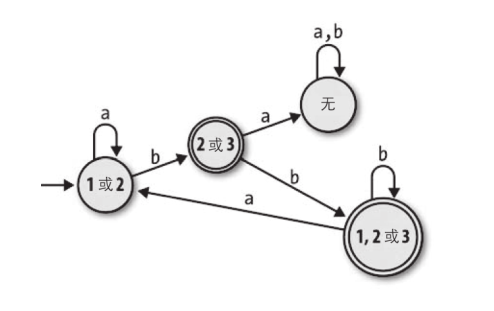
4. 从NFA转为DFA

我们已经了解NFA和DFA，仔细的研究NFA，思考它和DFA有什么区别吗？之后观察下图：

如果我们把一个NFA用上面的这种形式表现出来，那么它是不是就变成了一个DFA了呢？答案是肯定的。通过上图的这种转化方式，我们可以将任意一个NFA转化为DFA，具体的实现就不给出了，读者有兴趣可以自己实现。如果觉得有困难，可以参考计算的本质的3.4节。

5. 总结

有限自动机是一种非常简单但是又很重要的计算模型，我们后面提到的下推自动机和图灵机都是在有限自动机的基础上构造的，所以在查看后面的文章前请务必要先理解有限自动机这种计算模型。