在计算机科学中,存在着表、树、图等等这样的常见数据结构。相较于一维的表,树存在着很多的优势。树的定义参见维基百科
树(英语:tree)是一种抽象资料型别(ADT)或是实作这种抽象资料型别的数据结构,用来模拟具树状结构性质的资料集合。它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
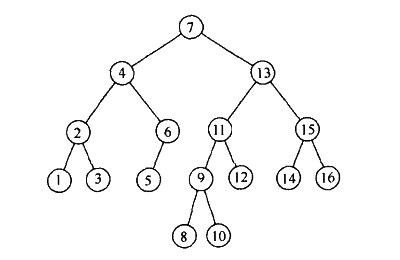
下图是一个典型的树
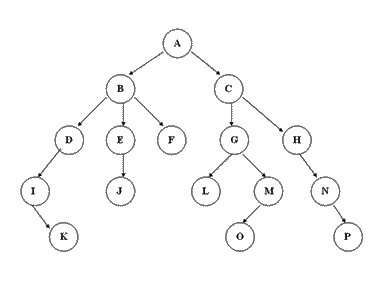
如果一个树它的任意一个节点的子节点数都不超过两个,那我们就称这个树为二叉树。二叉树存在着一些特殊的性质,同时因为可以通过儿子-兄弟-表示法把任意一个树转化为二叉树,所以树问题的研究最终都可以简化为对二叉树的研究。
1.二叉查找树
如果一个树是二叉树,同时对于这个树的每一个节点,该节点的左子树中的所有节点的值都小于该节点的值;该节点的右子树中的所有节点的值都大于该节点的值,那我们就可以称这个树是二叉查找树。
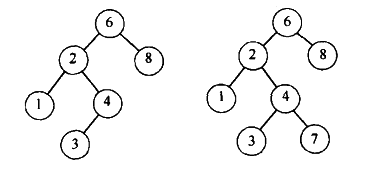
如上图所示,只有左边的是二叉树,右边的树的节点 7 的值大于 6,所以不是二叉查找树。
二叉查找树一般会有contains、insert、remove、findMin、findMax等等这样的操作,而且一般都可以通过递归来完成以上操作。这里需要着重讲解的是remove操作,该操作相对于其他操作而言略显复杂。
remove操作所对应的节点可以被归为三类,分别是:
叶子节点,对于这种情况,只需要直接删除该节点即可;
含有一个子节点的节点,此种情况需要把原本指向该节点的指针指向其原本所拥有的唯一子节点即可;
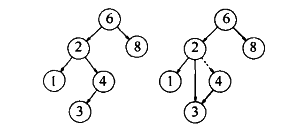
有两个子节点的情况,此种情况稍微复杂一些。解决方式是在该节点的左子树中找出最大值(或者在右子树中找到最小值),然后把找到的节点的值赋给此要删除的节点,最后删除之前所找到的最大值(或最小值)的节点(因为此节点必然是叶子节点,所以此问题变成了叶子节点的删除问题)。
因为左子树中的最大值(或者右子树中的最小值)必然大于左子树中的所有的值并且小于右子树中的所有值,所以可以保证二叉查找树的性质不变。
下面是 Java 实现二叉查找树的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
| public class BinarySearchTree {
private class BinaryNode {
int value;
BinaryNode left;
BinaryNode right;
BinaryNode(int value, BinaryNode left, BinaryNode right) {
this.value = value;
this.left = left;
this.right = right;
}
}
private BinaryNode root;
public BinarySearchTree() {
root = null;
}
public void empty() {
root = null;
}
public boolean isEmpty() {
return root == null;
}
public boolean contains(int value) {
return contains(value, root);
}
private boolean contains(int value, BinaryNode node) {
if (node == null)
return false;
if (value < node.value) {
return contains(value, node.left);
} else if (value > node.value) {
return contains(value, node.right);
} else {
return true;
}
}
public int findMin() throws Exception {
if (root == null)
throw new Exception("root is null");
BinaryNode node = root;
while (node.left != null)
node = node.left;
return node.value;
}
public int findMax() throws Exception {
if (root == null)
throw new Exception("root is null");
BinaryNode node = root;
while (node.right != null)
node = node.right;
return node.value;
}
public void insert(int value) {
root = insert(value, root);
}
private BinaryNode insert(int value, BinaryNode node) {
if (node == null)
return new BinaryNode(value, null, null);
if (value < node.value) {
node.left = insert(value, node.left);
} else if (value > node.value) {
node.right = insert(value, node.right);
}
return node;
}
public void remove(int value) {
root = remove(value, root);
}
private BinaryNode remove(int value, BinaryNode node) {
if (node == null)
return null;
if (value < node.value) {
node.left = remove(value, node.left);
} else if (value > node.value) {
node.right = remove(value, node.right);
} else {
if (node.left != null && node.right != null) {
BinaryNode rightMin = node.right;
while (rightMin.left != null)
rightMin = rightMin.left;
node.value = rightMin.value;
node.right = remove(rightMin.value, node.right);
} else {
node = (node.left != null) ? node.left : node.right;
}
}
return node;
}
public void echo() {
String space = "|----- ";
echo(root, space);
}
private void echo(BinaryNode node, String space) {
if (node != null) {
System.out.println(space + node.value);
space = "| " + space;
echo(node.left, space);
echo(node.right, space);
}
}
public static void main(String[] args) throws Exception {
BinarySearchTree tree = new BinarySearchTree();
tree.insert(2);
tree.insert(1);
tree.insert(3);
tree.insert(4);
tree.insert(-1);
tree.echo();
System.out.println(tree.findMin());
System.out.println(tree.findMax());
tree.remove(2);
tree.echo();
}
}
|
2.AVL 树
在前一节中,我们已经了解了如何构建一个二叉查找树以及如何对这个二叉查找树进行元素的增加、删除等等操作。但是这样的二叉查找树可能会存在性能上的问题,具体如下图所示:
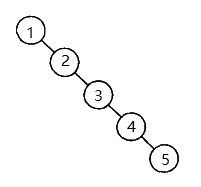
因为 1 < 2 < 3 < 4 < 5,并且除了 5 之外所有的节点都拥有一个子节点,所以这确实是一棵二叉查找树,但事实上这棵树却给人一种链表的感觉。二叉查找树的性能和树的高度密切相关,所以树的的高度越低,元素的操作速度越快。想要二叉查找树的高度低,那么就应该保证最好每个节点都能够拥有两个子节点才好,也就是像下图这样:
如上的树被称作AVL树,即带有平衡条件的二叉树。具体定义如下:
对于任何一个节点,其左子树和右子树的高度差不能超过 1 的二叉查找树。
显然 AVL 树可以降低一个普通二叉查找树的高度,所以我们需要做的就是把一个普通的二叉查找树转变为 AVL 树。因此我们需要在上面二叉查找树代码的基础上稍微做点修改:
- 给每个节点添加一个 height 属性(记录此节点的高度);
- 增添一个实现普通的树转化为 AVL 树的算法。
具体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
| public class AVLTree {
private class BinaryNode {
int value;
BinaryNode left;
BinaryNode right;
int height;
BinaryNode(int value, BinaryNode left, BinaryNode right) {
this.value = value;
this.left = left;
this.right = right;
height = 0;
}
}
private BinaryNode root;
public AVLTree() {
root = null;
}
public void insert(int value) {
root = insert(value, root);
root = avl(root);
}
private BinaryNode insert(int value, BinaryNode node) {
if (node == null)
return new BinaryNode(value, null, null);
if (value < node.value) {
node.left = insert(value, node.left);
} else if (value > node.value) {
node.right = insert(value, node.right);
}
node.height = Math.max(height(node.left), height(node.right)) + 1;
return node;
}
private BinaryNode avl(BinaryNode node) {
if (node != null) {
if (height(node.left) - height(node.right) == 2) {
if (node.left.left != null)
node = rotateWithLeftChild(node);
else
node = doubleWithLeftChild(node);
} else if (height(node.right) - height(node.left) == 2) {
if (node.right.right != null)
node = rotateWithRightChild(node);
else
node = doubleWithRightChild(node);
}
node.left = avl(node.left);
node.right = avl(node.right);
}
return node;
}
private BinaryNode rotateWithLeftChild(BinaryNode node2) {
BinaryNode node1 = node2.left;
node2.left = node1.right;
node1.right = node2;
node2.height = Math.max(height(node2.left), height(node2.right)) + 1;
node1.height = Math.max(height(node1.left), node2.height) + 1;
return node1;
}
private BinaryNode doubleWithLeftChild(BinaryNode node3) {
node3.left = rotateWithLeftChild(node3.left);
return rotateWithLeftChild(node3);
}
private BinaryNode rotateWithRightChild(BinaryNode node2) {
BinaryNode node1 = node2.right;
node2.right = node1.left;
node1.left = node2;
node2.height = Math.max(height(node2.right), height(node2.left)) + 1;
node1.height = Math.max(height(node1.right), node2.height) + 1;
return node1;
}
private BinaryNode doubleWithRightChild(BinaryNode node3) {
node3.right = rotateWithRightChild(node3.right);
return rotateWithRightChild(node3);
}
private int height(BinaryNode node) {
return node == null ? -1 : node.height;
}
public void echo() {
String space = "|----- ";
echo(root, space);
}
private void echo(BinaryNode node, String space) {
if (node != null) {
System.out.println(space + node.value);
space = "| " + space;
echo(node.left, space);
echo(node.right, space);
}
}
public static void main(String[] args) throws Exception {
AVLTree tree = new AVLTree();
tree.insert(1);
tree.insert(2);
tree.insert(3);
tree.insert(4);
tree.insert(5);
tree.insert(6);
tree.insert(7);
tree.insert(8);
tree.insert(9);
tree.insert(10);
tree.insert(11);
tree.insert(12);
tree.insert(-5);
tree.echo();
}
}
|
如上所示,添加了height参数用来记录节点高度,并且实现了 AVL 算法。对于任意一个未平衡的节点,其可能存在四种情况:左节点的左节点过高、左节点的右节点过高、右节点的右节点过高、右节点的左节点过高,分别对应了代码中的四种转化实现方式。
这样一来我们就实现了一个把普通二叉查找树转化为 AVL 树的算法,并且在每次插入操作执行完之后立即执行转化操作,所以即使插入导致树变形也可以立即使其恢复为 AVL 树。
这里在实现 AVL 的时候是把其单独提出来作为一个独立的函数来完成的,并且是在插入操作结束后再执行一次 AVL 函数来完成整个操作。但是,仔细观察可以发现,插入操作和 AVL 算法都是通过对一棵树进行反复递归来实现的,所以上面这种实现方式相当于我们对树做了两次的递归(插入递归一次、AVL 函数递归一次),这实际上是对资源的浪费,我们完全可以在一次的递归中就完成插入和树结构的变化操作,具体实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| public void insert(int value) {
root = insert(value, root);
}
private BinaryNode insert(int value, BinaryNode node) {
if (node == null)
return new BinaryNode(value, null, null);
if (value < node.value) {
node.left = insert(value, node.left);
if (height(node.left) - height(node.right) == 2)
if (value < node.left.value)
node = rotateWithLeftChild(node);
else
node = doubleWithLeftChild(node);
} else if (value > node.value) {
node.right = insert(value, node.right);
if (height(node.right) - height(node.left) == 2)
if (value > node.right.value)
node = rotateWithRightChild(node);
else
node = doubleWithRightChild(node);
}
node.height = Math.max(height(node.left), height(node.right)) + 1;
return node;
}
|
如上,我们成功的把 AVL 算法整合到了 insert 操作中,提高了程序的效率,但是可能不如前面的那个实现方式那样好理解,并且如果要添加删除功能,那么前面的方法可在删除操作执行完毕之后直接使用,无需增加新的代码。
总结:
二叉查找树与 AVL 树都是非常重要的数据结构,并且 AVL 树存在着更好的执行效率,这两种数据结构都应该需要能够熟练的掌握。
本文链接: https://www.nosuchfield.com/2016/09/06/binary-search-tree-with-AVL-tree/




