有穷自动机（finite automation，FA），也叫做有限状态自动机，是一种在计算机学领域非常重要的计算模型。

1.有穷自动机

我们先看一个有穷自动机 M：

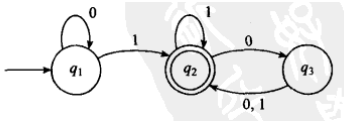
接下来，我们可以用形式化的方式来描述这个FA：M=(Q, Σ, δ, q0, F)

其中：

  • Q = {q1, q2, q3}

  • Σ = {0, 1}

  • δ 描述为

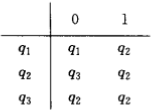
  • q1 是起始状态

  • F = {q2}

根据以上规则，我们已经可以定义一个 FA 了。其中：

  1. Q 表示的是该状态机所有的状态，即该 FA 所有的存在的状态都包含在此集合中

  2. Σ 表示的是所有的输入状态的集合，即所有可能的输入都包含在之中

  3. δ 描述的函数关系式，即从某一个状态转移到另一个状态时所遵循的规则

  4. q1 是起始状态，即该 FA 最开始的时候的状态

  5. F 是接受状态，或者也称为最终状态，无论一个状态机经过了怎样的变换，最后的一部转移必须转移到接受状态，否则就是非法的。符合这种转移要求的语言是可以被此台 FA 识别的，被称为正则语言。

2.确定型有穷自动机与非确定型有穷自动机

确定型有穷自动机（DFA）：每个状态对于字母表中的每一个符号总是恰好有一个转移箭头射出

非确定型有穷自动机（NFA）：一个状态对于字母表中的每一个符号可能有 0 个、1 个或多个箭头，NFA 中还可以存在有带有标号 ε 的箭头

  • 每一台 NFA 都可以转换成一台等价的 DFA，而构造 NFA 有时比直接构造 DFA 容易

  • 如果两台机器识别同样的语言，则称他们是等价的；每一台非确定型有穷自动机都等价于某一台确定型有穷自动机

参考文献：计算理论导引 机械工业出版社 2006-7